Simplex noise is a type of gradient noise just like the Perlin noise. Infact, the creator of both noises is the same person–Kenneth [Ken] Perlin. Ken thought that his implementation of perlin noise is not good enough, especially in higher dimensions, so he came up with a better algorithm to address the limitation of classic noise function. So simplex is better, what else? Obviously I am not going into the details of the algorithm (Stefan Gustavson already does the job far better than I ever could), but let me just say how simplex performs better than the perlin noise.
- simplex noise requires fewer multiplications and scales to higher dimensions (4D and up) with much less computational cost, the complexity is $O(n^2)$ for $n$ dimensions instead of $O(2^n)$ of perlin noise.
- simplex noise has no visually-significant directional artifacts.
For a high-level overview, it’s enough to know that the algorithm uses something known as a simplex grid to add nearby values and produce numbers between -1 and 1 that look linearly-interpolated like classic Perlin noise. How these grids are selected?
For a space with $N$ dimensions, pick the simplest and most compact shape that can be repeated to fill the entire space. A straight line segment is a 1D simplex. A triangle is a 2D simplex. A square is not a 2D simplex, because it has one more corner and side than a triangle and this isn't the simplest possible shape. A straight line segment is also not a 2D simplex, because it has only a single dimension, no matter how it is oriented in 2D space. Finally, a tetrahedron is a 3D simplex. In general, a simplex shape for $N$ dimensions has $N+1$ corners.
I implemented OpenSimplexNoise for two-dimensional as OpenSimplex is patented. I stole the permutation table from Stefan Gustavson’s paper and refashioned the code in python.
import math
# gradient table for 2D noise
grad3 = [
[1,1,0], [-1,1,0], [1,-1,0], [-1,-1,0],
[1,0,1], [-1,0,1], [1,0,-1], [-1,0,-1],
[0,1,1], [0,-1,1], [0,1,-1], [0,-1,-1]
]
# permutation table
perm = [
151,160,137,91,90,15,131,13,201,95,96,53,194,233,7,225,
140,36,103,30,69,142,8,99,37,240,21,10,23,190,6,148,
247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,
57,177,33,88,237,149,56,87,174,20,125,136,171,168,68,175,
74,165,71,134,139,48,27,166,77,146,158,231,83,111,229,122,
60,211,133,230,220,105,92,41,55,46,245,40,244,102,143,54,
65,25,63,161,1,216,80,73,209,76,132,187,208,89,18,169,
200,196,135,130,116,188,159,86,164,100,109,198,173,186,3,64,
52,217,226,250,124,123,5,202,38,147,118,126,255,82,85,212,
207,206,59,227,47,16,58,17,182,189,28,42,223,183,170,213,
119,248,152,2,44,154,163,70,221,153,101,155,167,43,172,9,
129,22,39,253,19,98,108,110,79,113,224,232,178,185,112,104,
218,246,97,228,251,34,242,193,238,210,144,12,191,179,162,241,
81,51,145,235,249,14,239,107,49,192,214,31,181,199,106,157,
184,84,204,176,115,121,50,45,127,4,150,254,138,236,205,93,
222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
] * 2 # avoid index out of range
def fastfloor(x):
return int(math.floor(x))
def dot(g, x, y):
return g[0] * x + g[1] * y
def fade(t):
return t * t * t * (t * (t * 6 - 15) + 10)
def noise2d(xin, yin):
n0, n1, n2 = 0.0, 0.0, 0.0 # noise contributions from the three corners
# skew the input space to determine which simplex cell we're in
F2 = 0.5 * (math.sqrt(3.0) - 1.0)
s = (xin + yin) * F2
i = fastfloor(xin + s)
j = fastfloor(yin + s)
G2 = (3.0 - math.sqrt(3.0)) / 6.0
t = (i + j) * G2
X0 = i - t
Y0 = j - t
x0 = xin - X0
y0 = yin - Y0
# determine which simplex we are in
if x0 > y0:
i1, j1 = 1, 0 # lower triangle
else:
i1, j1 = 0, 1 # upper triangle
x1 = x0 - i1 + G2
y1 = y0 - j1 + G2
x2 = x0 - 1.0 + 2.0 * G2
y2 = y0 - 1.0 + 2.0 * G2
# work out the hashed gradient indices
ii = i & 255
jj = j & 255
gi0 = perm[ii + perm[jj]] % 12
gi1 = perm[ii + i1 + perm[jj + j1]] % 12
gi2 = perm[ii + 1 + perm[jj + 1]] % 12
# calculate the contribution from the three corners
t0 = 0.5 - x0 * x0 - y0 * y0
if t0 < 0:
n0 = 0.0
else:
t0 *= t0
n0 = t0 * t0 * dot(grad3[gi0], x0, y0)
t1 = 0.5 - x1 * x1 - y1 * y1
if t1 < 0:
n1 = 0.0
else:
t1 *= t1
n1 = t1 * t1 * dot(grad3[gi1], x1, y1)
t2 = 0.5 - x2 * x2 - y2 * y2
if t2 < 0:
n2 = 0.0
else:
t2 *= t2
n2 = t2 * t2 * dot(grad3[gi2], x2, y2)
# add contributions and scale to [-1,1]
return 70.0 * (n0 + n1 + n2)
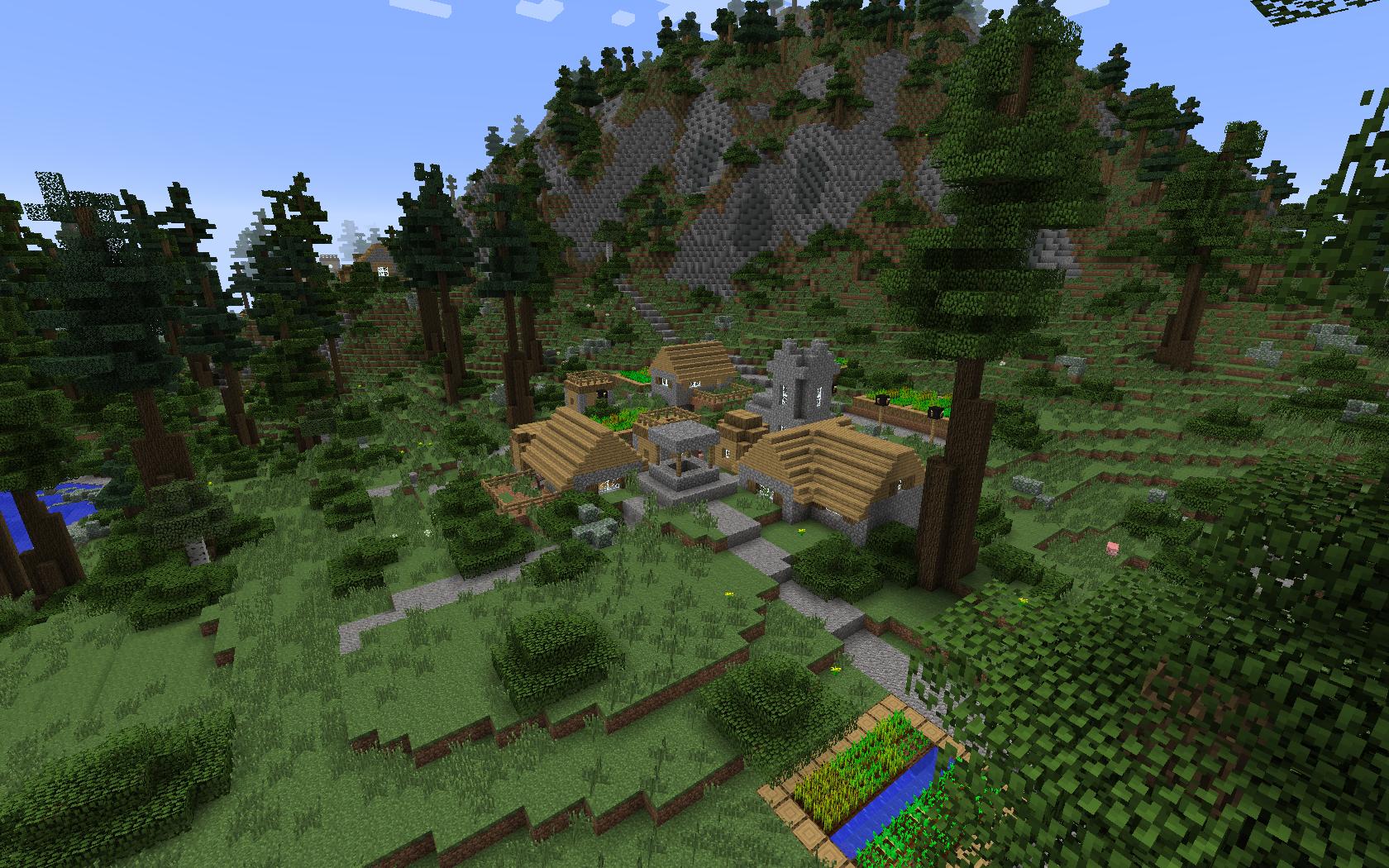
Here are some fractals that I created by stacking up octaves. This other one is on twitter.

