rope

RoPE (Rotary Positional Embeddings) introduces an innovative concept of applying rotation to word vectors, rather than adding position vectors. For example, in order to encode the position of this vector in a sentence with a two-dimensional vector of the word "dog", RoPE rotates this vector. The rotation angle (theta) is proportional to the position of the word in the sentence. As an example, rotate the vector at the theta in the first position, at 2 theta in the second position, and so on. This provides a more natural way to represent sequential information.

def rope(x, theta):
    # theta: (1, seq_len, 1) — angle per position
    batch, seq_len, dim = x.shape. # (batch, seq_len, dim) per attn head H
    assert dim % 2 == 0
    x1 = x[..., ::2]  # even dims
    x2 = x[..., 1::2]  # odd dims

    sin = torch.sin(theta)
    cos = torch.cos(theta)

    x_rotated = torch.stack([
        x1 * cos - x2 * sin,
        x1 * sin + x2 * cos
    ], dim=-1)
    return x_rotated.flatten(-2)  # (batch, seq_len, dim)

• Equivalent pytorch code (if you prefer summation and q, m are known). Note that equivalence here is referred to simplicity and flexibility and does not guarantee efficiency, especially when training large deep neural nets from scratch.

import torch
def apply_rope(q, thetas, m):
    # q: (d,), thetas: (d//2,), m: scalar
    q = q.view(-1, 2)  # (d/2, 2)
    angles = m * thetas
    cos = torch.cos(angles)
    sin = torch.sin(angles)

    rot = torch.stack([
        torch.stack([cos, -sin], dim=1),
        torch.stack([sin,  cos], dim=1)
    ], dim=1)  # (d/2, 2, 2)

    q_rotated = torch.einsum('bij,bj->bi', rot, q)  # (d/2, 2)
    return q_rotated.flatten()

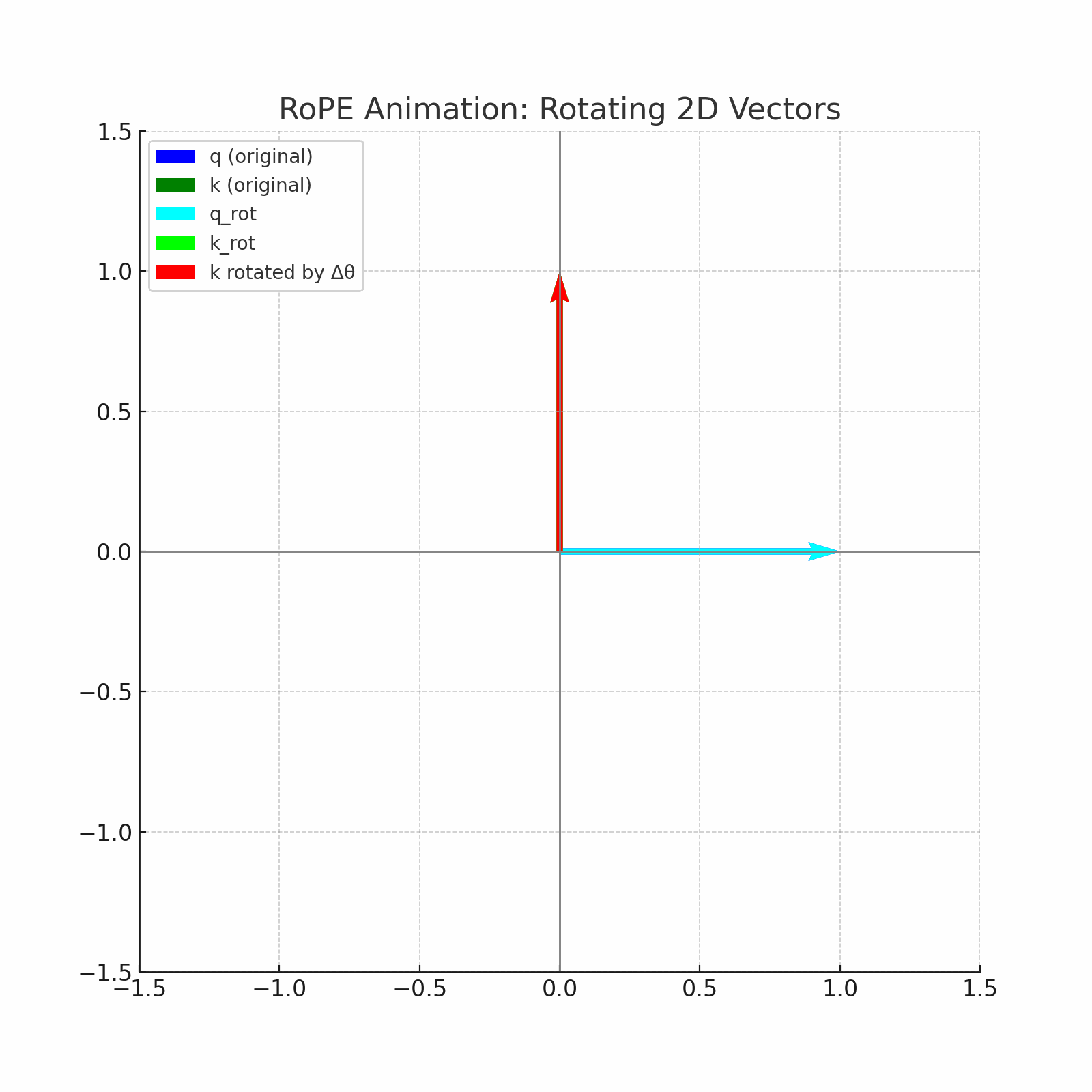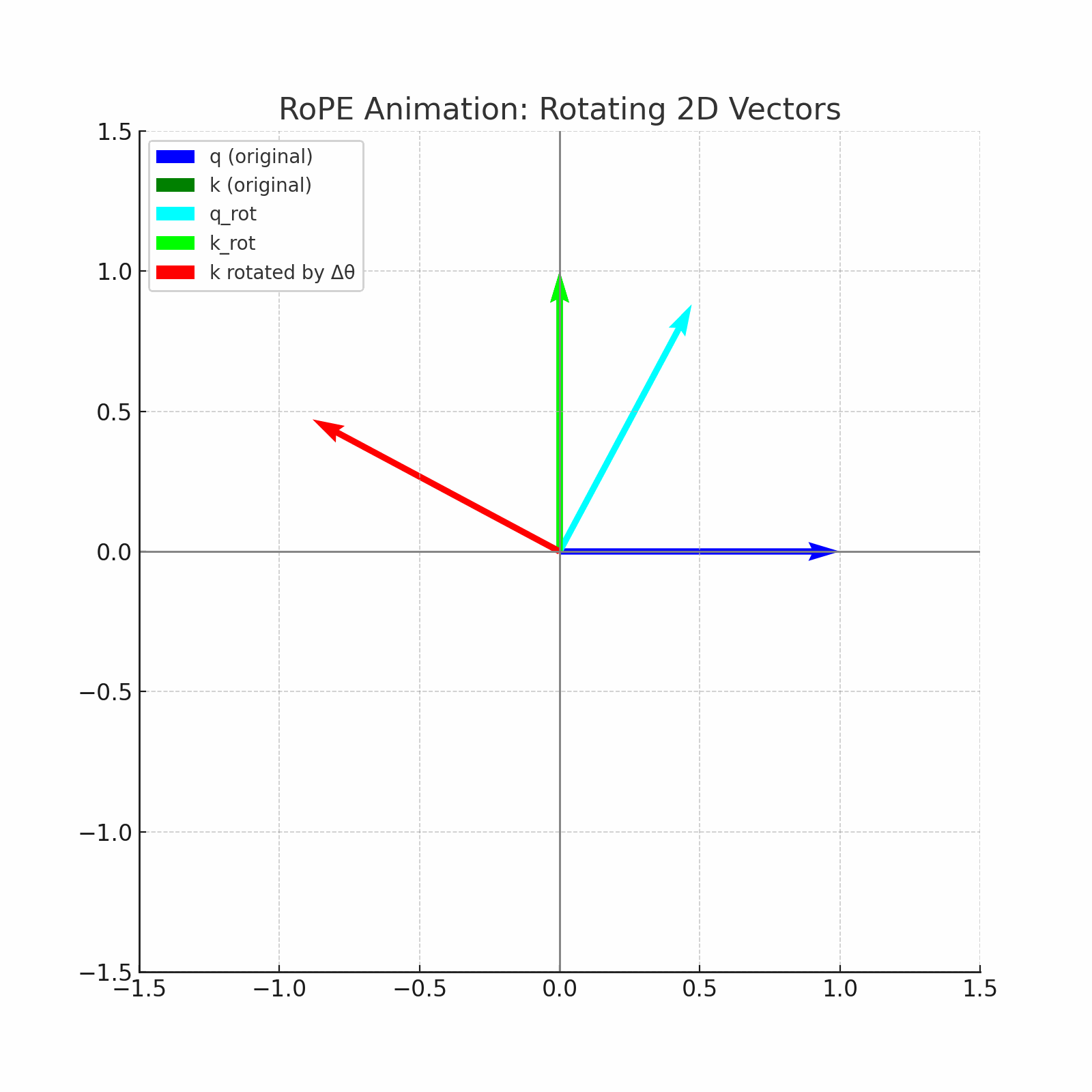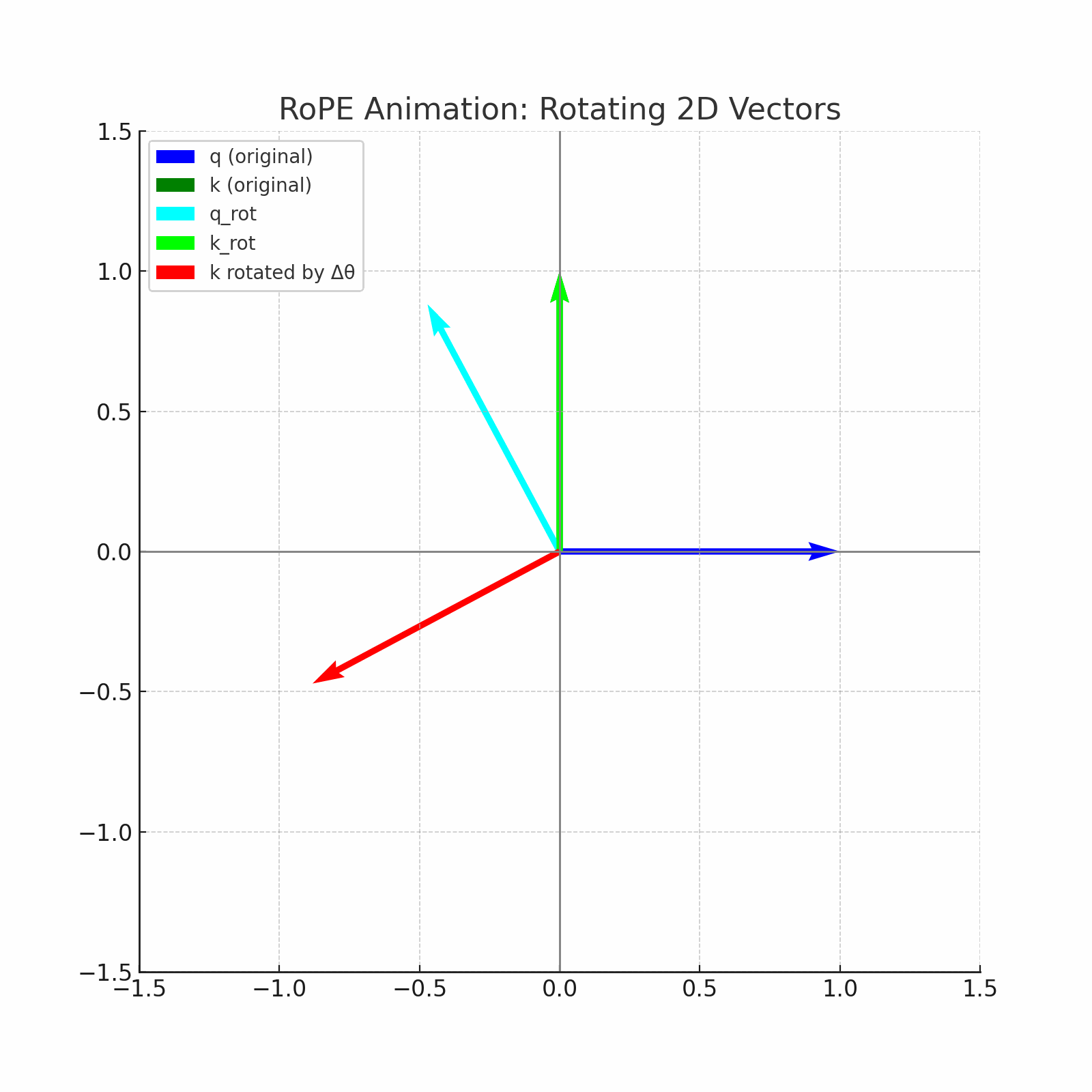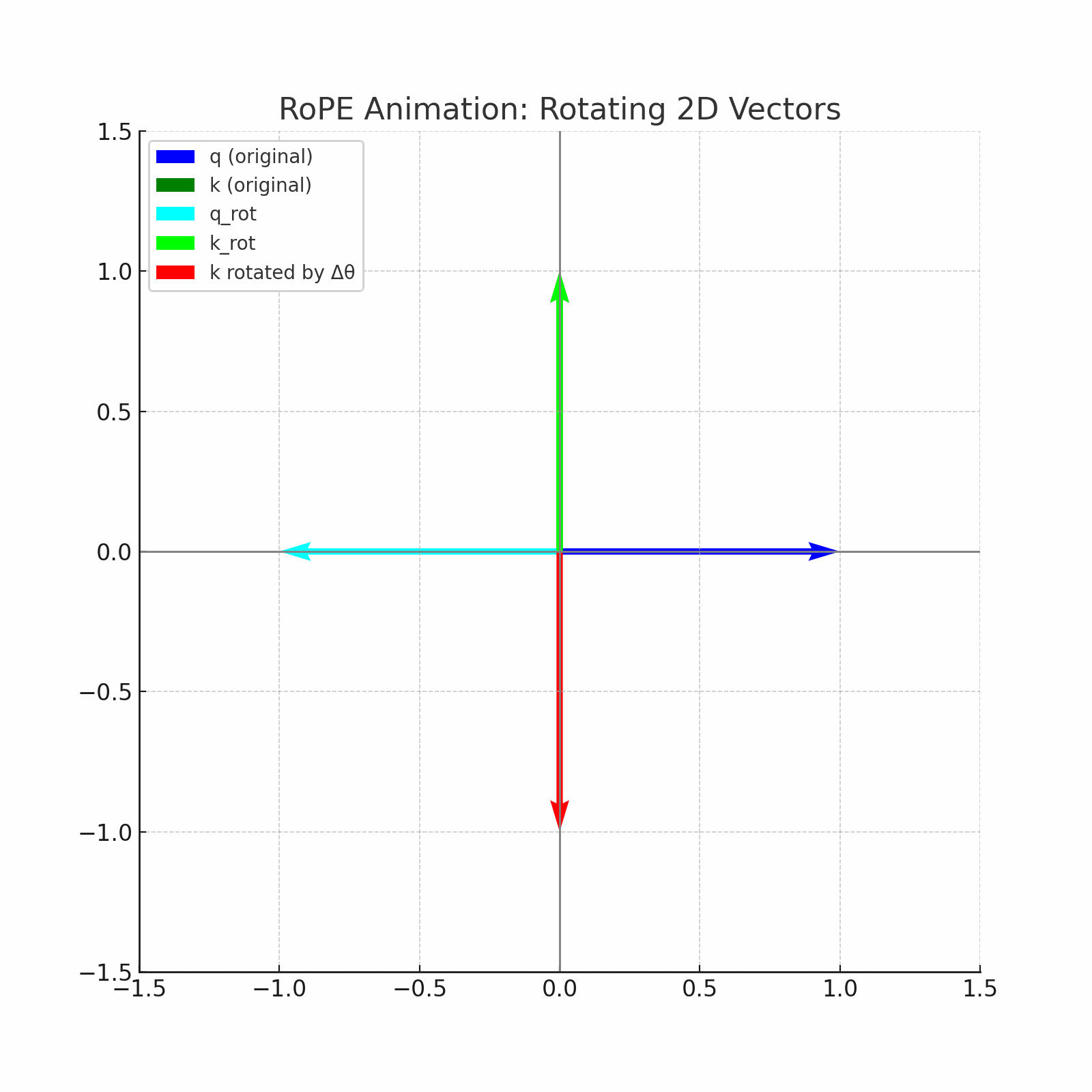
Fused RoPE kernel in metal

The implementation uses a fused kernel approach where each thread processes one rotation pair (even/odd elements), achieving optimal GPU utilization and memory coalescing.

kernel void fused_rope(
    device const float* input     [[ buffer(0) ]],
    device const float* cos_table [[ buffer(1) ]],
    device const float* sin_table [[ buffer(2) ]],
    device float*       output    [[ buffer(3) ]],
    constant uint&      S         [[ buffer(4) ]],
    constant uint&      B         [[ buffer(5) ]],
    constant uint&      H         [[ buffer(6) ]],
    constant uint&      D         [[ buffer(7) ]],
    uint3 gid                   [[ thread_position_in_grid ]])
{
    uint idx = gid.x;
    uint total_elements = S * B * H * (D / 2);

    if (idx >= total_elements) return;

    uint half_d = D / 2;
    uint d_pair = idx % half_d;
    uint remaining = idx / half_d;
    uint h = remaining % H;
    remaining = remaining / H;
    uint b = remaining % B;
    uint s = remaining / B;

    uint base_idx = ((s * B + b) * H + h) * D;

    uint even_idx = base_idx + 2 * d_pair;
    uint odd_idx = base_idx + 2 * d_pair + 1;

    float x_even = input[even_idx];
    float x_odd = input[odd_idx];

    float cos_val = cos_table[s * half_d + d_pair];
    float sin_val = sin_table[s * half_d + d_pair];

    output[even_idx] = x_even * cos_val - x_odd * sin_val;
    output[odd_idx] = x_even * sin_val + x_odd * cos_val;
}

When dispatching threads , dispatch with (S * B * H * D/2) threads in the x-dimension

MTLSize threadsPerGrid = MTLSizeMake(S * B * H * (D/2), 1, 1);

Until then… heavy caffeine ☕️ and peace ☮️