Large Language Models are Data Compressors

Language Models, or broadly speaking - any probabilistic model can, in principle, be used to compress data, as long as it can assign probabilities to data sequences.

When strictly talking about artificial or programming language, there is more than 50 years of work in the field of theory of computation which spans to other domains like information (Shannon, 1948) and model theory. Many programming languages are Turing complete, meaning that in principle they can represent any computable function. This tells that they have no inherent limitation on what can be encoded - as long as the information is computable. However, Turing completeness is a binary attribute (either a language is Turing complete or not) and doesn’t offer a quantitative measure of “how much” one can compress or express information beyond that universality. For Turing complete languages, “Kolmogorov complexity” provides an inherent lower bound on how much a piece of data can be compressed. The twist is that Kolmogorov complexity is uncomputable in general; that is, there is no algorithm that can, for every string, produce this minimal description length.

Arithmetic Encoding is a lossless compression where there is no loss in quality when reconstructing (or decompressing) the message. It is an entropy-based algorithm that uses a low number of bits to compress data.

Analogous to how a predictive distribution can be used for lossless compression via arithmetic coding, any compressor can be employed for sequence prediction. The main idea is to use the compressor to estimate a probability distribution over the next symbol, given the preceding sequence. The model with the lowest compressed file size (in bits) is the one that best predicts the sequence, and thus can be considered the “best” model. This leads to the principle of Minimum Description Length (MDL), which states that the best model for a set of data is the one that minimizes the sum of:

1. The length of the description of the model (in bits).

1. The length of the description of the data, when encoded with the help of the model (in bits).

Shannon’s Source Coding Theorem

The theorem establishes a fundamental limit on the number of bits needed to represent a sequence of symbols from a source. It states that the average number of bits per symbol required for lossless compression is at least the entropy of the source. For a source with probability distribution p(x) over a set of symbols, the entropy is given by:

$$H(X) = - \sum_{i} p(x_i) \log_2 p(x_i)$$

This entropy represents the average amount of information (in bits) per symbol. A good compressor will assign shorter codewords to more probable symbols and longer ones to less probable symbols, thus achieving an average codeword length close to the entropy. This implies that a model which can compress data well must have learned the underlying probability distribution of the data effectively.

A brief example:

> text = "hello world"
> compressed_text = gzip.compress(text.encode())
> print(len(compressed_text))

The above code will output a length of 21 bytes. But if we try to predict this using a GPT-2 model, the compressed size is lower. This illustrates that a better probabilistic model (like GPT-2) leads to better compression.

Predict to Compress

The core idea is to encode each symbol based on the probability assigned to it by the model, conditioned on the preceding symbols. The number of bits required to encode a symbol x_i, given the context of previous symbols, is given by:

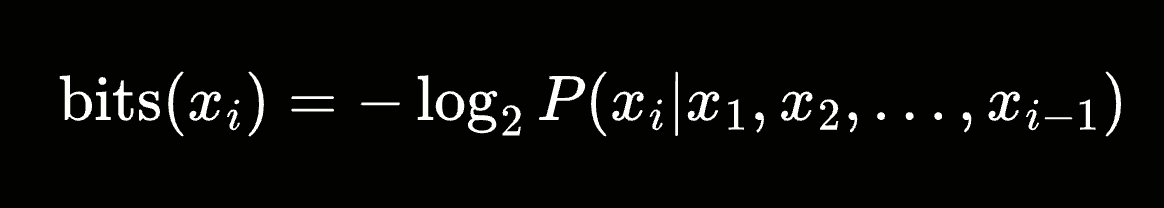
This is the self-information of the symbol. The total compressed size of a sequence is the sum of the self-information of all its symbols.

Is Prediction == Compression?

Yes. A model’s ability to predict the next token in a sequence is directly proportional to its ability to compress that sequence. For example, if a model can predict the next word with 90% accuracy, it means that the model has learned the underlying patterns in the data so well that it can effectively “summarize” the information in a compressed form. When a model is trained to minimize its prediction error (e.g., using cross-entropy loss), it is implicitly learning a compressed representation of the data. The parameters of a trained language model can be seen as a compressed summary of the statistical patterns observed in the training corpus.

---

Resources

1. The theoretical minimum for compression is given by the entropy of the data source.

1. The Intuition Behind Shannon’s Entropy

1. Andrej Karpathy’s video on tokenization provides a great high-level overview.

1. A good language model is a good compressor, and vice-versa. This is not a coincidence, but a deep connection rooted in information theory. So next time you see a language model generating fluent text, remember that you are also looking at a very powerful data compressor.